Although it's not at all obvious to most, the speed you drive has a highly significant effect on the fuel consumption of your vehicle. The key is the drag equation, which is an approximation of the drag force on an object moving at high speed (relative to the characteristics of the fluid in which it's moving - more on that later).
The drag equation is

where F represents the force, rho is the density of the fluid, v is the velocity of the fluid with respect to the object (in the case of a car, it's equivalent for us to consider the car in motion and the fluid stationary), and A is the cross-sectional area of the surface relative to the fluid - for us, the "face" of the car moving into the "wind." The C term is the drag coefficient, which is a "fudge factor" that's usually determined empirically and depends on the properties of the surface, its shape, and the properties of the fluid*.
The key to take away from the drag equation is that the drag force depends on the square of velocity. However, if we want to talk about fuel consumption (call it gasoline in gal/min), we're going to need to move beyond just the drag force. We can compare gasoline consumption at different speeds by using the energy requirement of your car, in, say, horsepower. Horsepower is a power term (in case the name didn't make it obvious), meaning it expresses some amount of energy expended over some period of time**.
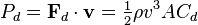 We can relate the force to the power required to overcome it by using the definition of work (a force exerted over a distance) and diving by the total time. Since the distance over which you travel divided by the time over which you travel is your average velocity, this gives the power equation above***. Note now that the power is proportional to the cube of velocity.
We can relate the force to the power required to overcome it by using the definition of work (a force exerted over a distance) and diving by the total time. Since the distance over which you travel divided by the time over which you travel is your average velocity, this gives the power equation above***. Note now that the power is proportional to the cube of velocity. So now, onto why I drive below the speed limit. One fine day I was driving from Ithaca, NY to Syracuse, NY, on the I-81N out of Cortland. The road is pretty boring except for the occasional deer, so I did some mental math. Because the fuel consumption (power) required from my car to overcome drag is proportional to the cube of velocity, the ratio of fuel consumption at, say, 75 mph vs at 65 mph is simply (75^3)/(65^3).
The ratio turns out to be about 1.54. This means that to a first approximation, at 75 mph I was consuming fifty percent more fuel than I was at 65 mph! Ouch. I knew that on country roads, my Subaru got about 23 mpg at 65 mph, which means that over a 60 mile drive at around 65 mph it'd consume roughly 3 gallons. At 75, it'd be consuming 1.5 more gallons. But wait - I was saving time by driving faster. Was my time worth it?
This calculation was easier - between 75 and 65, over the course of an hour it'd take (60/75) hours (0.8 hours, or 48 minutes) to go at 75 mph versus 60/65 hours (0.92 hours, or 55 minutes and about 20 seconds) to go at 65 mph. How much was 7 minutes of my time worth? At the wages I was working at that point (about $15 an hour), $1.75. How much was 1.5 gallons of gas worth? At that time, roughly $6.
I decided to drive slower. However, on the way back, I had my girlfriend, which meant I, ahem, valued the time saved from driving faster more. I drove faster on the way back.
To this day I've yet to make enough money in hourly terms to justify regularly driving 75 mph over driving 65 mph on the highway. At the current average gasoline price in New York state ($3.92/gal), I'd have to be making $50.40 an hour to justify it, which for a standard 8-hour work week is $104,832 per year.
------
This analysis is relatively simple. There are a couple of (to my mind, anyway) interesting little wrinkles to this calculation, the magnitude of which I can't calculate off the top of my head but I think on balance points to even more fuel consumption at higher speed.
The first wrinkle occurs when we relax the assumption that the drag coefficient is the same at different velocities. Earlier, we assumed that the drag coefficient is the same at 75 mph and 65 mph - at least, I didn't call attention to the variation, which means I assumed the drag coefficient was the same. If we relax that assumption, it turns out that there's an additional velocity dependence in the drag equation. The drag coefficient is proportional to some power of the Reynolds number, which for an object moving through fluid is proportional to velocity. Usually the expression is something along the lines of C_d = k*Re^a, where k is some constant that's empirically determined and a is some number below 1, also empirically fit. So the power equation is actually proportional to velocity to the (3+a) power. So power required to overcome drag force is actually somewhat higher because of this effect.
The second wrinkle occurs when you consider that an engine doesn't linearly deliver horsepower with increasing fuel consumption. Engines have power curves that describe their performance given the acceleration they must deliver and the rpm they are already moving at. A power curve for the motor on a Kia Alto (a small car) is shown below:
Fuel consumption is the bottom curve (PS is a German abbreviation, common in the car industry, for metric horsepower). Most cars will operate in the downward sloping part of the curve (we usually change gear if we're not), which means that if we increase speed and don't change gears, fuel consumption per amount of energy delivered actually goes down. However, we're still delivering a much higher amount of energy, and the ratio varies (in the region we're likely to see) from about 4.5 to maybe 3.25. In reality the difference in engine RPM is likely to just be the ratio of the velocities, 75/65 or about 1.15, while the fuel consumption ratio occurs over a much larger range (about 3.5). Still, it means that the fuel consumption at higher velocities, all things being equal, is lower than we might expect because fuel consumption increases less than linearly.
Finally, we have to consider that engine work is also used to overcome rolling resistance in addition to drag. Rolling resistance is a subject that I don't have any experience in, but I know that for a car it generally increases at a much higher than one-to-one rate with applied torque. This has much more to do with the way the wheels interact with the pavement then the way bearings behave; at high speeds there's some slippage and the like that cause inefficiencies. If it were the bearings alone, we'd actually expect less resistance as speed increases because bearing lubricants tend to be shear thinning. But all in all, this causes required power and hence, fuel consumption to increase at higher velocity more than we would expect from drag alone.
edit: Thanks to a lively discussion with my friend Tom, here's some more interesting stuff:
Tom calculated that the optimal speed at my then wage of $15 by minimizing the total cost of a 60 mile journey:
Cost(v) = Gas cost + Time Cost
C(v) = (60/23) gal*$4/gal*(v^3/(65mph)^3) + $15/hr* 60 miles/v
C(v) = $10.43 * v^3/(65 mph)^3 + $900 mi/hr / v
The local minimum for this can be calculated with some basic calculus, but we were lazy and used Wolfram Alpha:
This means that my optimal speed at that wage, assuming that the drag force dominated my costs, was 53 mph. It turns out that's a pretty darn good assumption.
Thanks to some quick googling, I found the following diagram (which is given for a parcel truck):
Rolling resistance increases with a relatively low order with respect to velocity while aerodynamic drag has (as we've discussed) a very high order with respect to velocity. Thus at high speeds it's a bit tricky to discuss aerodynamic drag as the only force, but it isn't an overwhelmingly bad assumption. Note that on the above graph, the curves stop at about 120 kph which is about 75 mph.
All in all, a fun physics problem.
* The drag coefficient for most objects is close to 1. It's a measure of how close the object is to representing an ideal object for modeling, usually something like a cylinder of infinite height or some such. Most objects don't deviate much from that - hence, the coefficient doesn't modify the ideal equation much. For cars, though, a considerable amount of R&D goes into making that drag coefficient lower. In terms of fluid properties, however, it's also related to the Reynolds number, a dimensionless quantity that is related to the inertia of a fluid (usually involving the velocity) and the viscosity.
** It's easy to get confused about what quantity to look for when talking about fuel consumption, but we can review the units to double check: fuel burned releases energy (in joules) over time (min), while force (Newtons) must be multiplied by distance (Newton*meter = Joule) and divided by time (min) to produce an equivalent quantity.
*** Strictly speaking, if we wanted to be precise then the power equation should be given by d/dt(F_d \dot x), where F_d and x (the distance) are both vector quantities and d/dt is the differential operator with respect to time. This gives the instantaneous power consumption, which given the data for a whole trip can be averaged out taking into account all acceleration and deceleration and the like. However, for a rough comparison of fuel consumption at constant speeds it's not necessary.


No comments:
Post a Comment